I had a garbled understanding of Transformer architecture after consulting blogs, videos and coursera course. What made it finally clicked for me is Stanford CS 224N lecture by John Hewitt. He does a phenomenal job and I will strongly encourage to check it out. If you work with LLM’s the 1 hour and 17 minutes is worth the time investment.
Stanford CS224N NLP | Lecture 8 - Self-Attention and Transformers
Before diving into the details of transformer a little history.
Motivation for Transformers
Prior to introduction of Transformers, the state of the art algorithm for acheiving state of the art results on various NLP tasks were RNN’s and its variants e.g LSTM, BiDirectional LSTM etc. While the sequential nature of RNN lend itself well to modelling sequential data, it had some issues. The major ones being the following.
a). Linear interaction distance
b). Lack of parallelizability
Transformer solve the above problems but have their own issues which will come up later. Transformer is illustrated by the diagram below.
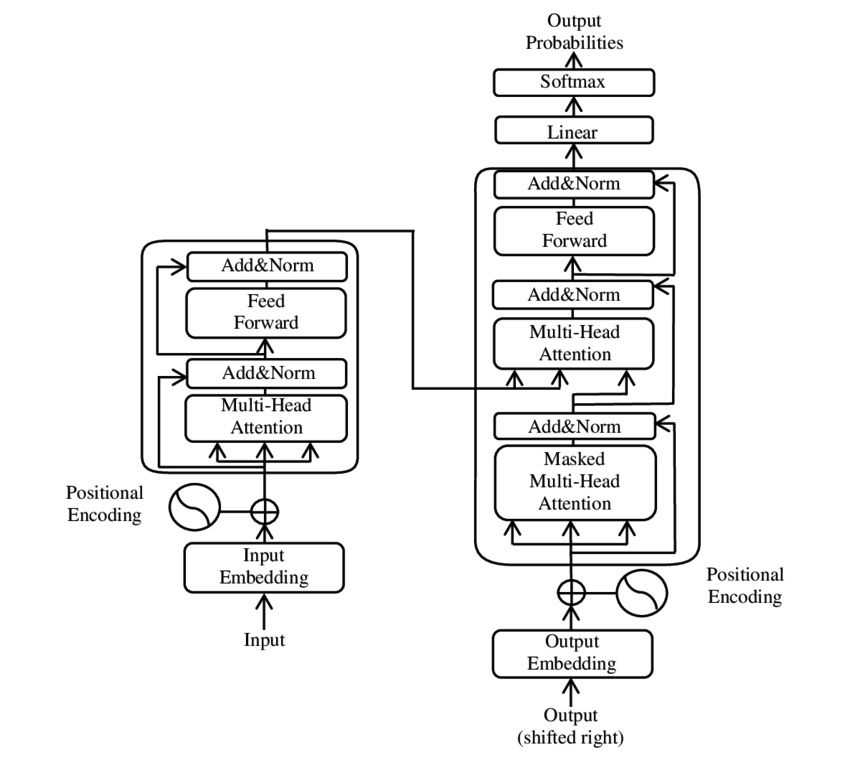
The diagram is complex but when approached as a submodules the algorithm is composed of its starts to make sense. In this note the submodule we will look at is Self-Attention.
The words from natural language go through a text tokenizer. Numerous technqiues exist for tokenize, but a very common method for tokenizing text is byte pair encoding. Here is a good explainer for byte pair encoding.
The tokenizer will transform a sentence into a list of numeral integers or a list of tokens. Given a token \(x_i\) in the list of tokens \(x_1:n\) we define a query \(q_i = Qx_i\), for matrix Q. A vector key and value are also needed such that \(k_i = Kx_i\) and \(v_i = Vx_i\).
The eventual representation of the list of tokens \(h_i\) is dot product of the value of the sequence. \[ h_i = \sum_{j=1}^{n} \alpha_{ij} v_j, \] The weights \(\alpha_{ij}\) selects the data to pull up. The weights are defined by calculating the relation between key and query \(q_i^Tk_j\) and calculating the softmax over the sequence. \[ \alpha_ij = \frac {exp(q_i^T k_j)}{\sum_{j^`=1}^{n}exp(q_i^Tk_{j^`})} \]
Self-attention instead of using a fixed embedding for each token, leverages the whole sequence to determine what other tokens should represent \(x_i\) in context.
References:1). https://en.wikipedia.org/wiki/Transformer_(machine_learning_model)#/media/File:The-Transformer-model-architecture.png
2). Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin: “Attention Is All You Need”, 2017; arXiv:1706.03762
4). Stanford CS224N NLP | Self-Attention and Transformers
5). https://huggingface.co/learn/nlp-course/chapter6/5?fw=pt